A fórmula química para um composto obtido por análise de composição sempre é a fórmula empírica. Podemos obter a fórmula molecular da fórmula empírica se nós soubermos a massa molecular do composto. A fórmula molecular sempre será algum múltiplo inteiro da fórmula empírica (isto é, múltiplos inteiros das subscrições da fórmula empírica).
Ex: a Vitamina C (ácido ascórbico) contém 40,92% de C; 4,58% de H e 54,50% de O, em massa. A massa molecular experimentalmente determinada é 176u. Quais são as fórmulas empírica e molecular para o ácido ascórbico?
Em 100 gramas de ácido ascórbico, temos: 40,92 gramas de C; 4,58 gramas de H; 54,50 gramas de O. Isto nos dá os mols de cada elemento:
(40,92g C) x (1mol/12,011g)=3,407moles de C.
(4,58g H) x (1mol/1,008g)=4,544mols de H.
(54,50g O) x (1mol/15,999g)=3,406mols de O.
Determina-se a relação com menor número inteiro, dividindo-se cada valor pelo de menor quantidade de mols (3.406 moles do Oxigênio):
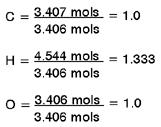
A quantidade relativa de mols de carbono e oxigênio parece ser igual, mas a quantia relativa de hidrogênio é mais alta. Considerando que não podemos ter “átomos fracionários” em um composto, nós precisamos normalizar a quantia relativa de hidrogênio para ser igual a um inteiro. 1.333 é 1 + 1/3, assim se multiplicarmos as quantias relativas de cada átomo por ‘3’, deveremos obter valores inteiros para cada átomo.
C = (1.0) x 3 = 3
H = (1.333) x 3 = 4
O = (1.0) x 3 = 3
ou, C3H4O3
Esta é a fórmula empírica para o ácido ascórbico. E a fórmula molecular? Falamos que, experimentalmente, foi determinada uma massa molecular de 176u.Qual é a massa molecular dafórmula empírica?
(3 x 12,011) + (4 x 1,008) + (3 x 15,999) = 88,062u.
A massa molecular da fórmula empírica é menor que a experimentalmente determinada. Qual é a relação entre os dois valores?
(176u /88,062u) = 2,0
Se multiplicarmos a fórmula empírica por ‘2’, então a massa molecular estará correta. Assim, a fórmula molecular é:
2 x C3H4O3 = C6H8O6
2.Do número de Avogadro, sabemos que há aproximadamente 6,02 x 1023 átomos/mol. Então, em 0,0142 mol temos :
(0,0142 mol) x (6,02 x 1023 átomos/mol) = 8,55 x 1021átomos
Volume molar de um gás
CNTP: temperatura = 0 °C e pressão =1atm.
É o volume ocupado pelo mol de moléculas de um gás qualquer nessas condições. Verifica-se, experimentalmente, que seu valor é praticamente o mesmo para qualquer gás, e situa-se em torno de 22,4 litros.
Essa constância no volume molar de um gás explica-se pelo fato de os tamanhos das moléculas gasosas serem desprezíveis quando comparados com o espaço vazio que há entre elas. Assim, se um balão de gás for enchido com 2g de gás hidrogênio (massa de 1mol de moléculas H2) e submetido à pressão externa de 1 atm e à temperatura de 0°C, ele adquirirá o volume de 22,432 litros. Substituindo o gás hidrogênio por 28g de gás nitrogênio(massa de 1mol de moléculas N2),o volume será de 22,403 litros, e assim por diante.
Logo: 1mol de gás 6,02 x 1023 moléculas 22,4 litros (CNTP)
Lei de Avogadro
Volumes iguais de dois gases, nas mesmas condições de temperatura e pressão, possuem o mesmo número de moléculas. Essa lei que foi a origem do conceito de molécula está implícita no conceito de volume molar (a CNTP), pois 22,4 litros de qualquer gás possuem 6,02 x 1023 moléculas.
Fórmula empírica (ou mínima)
Uma fórmula empírica conta as relações relativas de átomos diferentes em um composto (proporção). Assim, H2O é composto de dois átomos de hidrogênio e 1 átomo de oxigênio. Igualmente, 1.0 mol de H2O é composto de 2.0 mols de hidrogênio e 1.0 mol de oxigênio. Se sabemos as quantias molares de cada elemento em um composto, então podemos determinar a fórmula empírica.
Ex: o mercúrio forma um composto com o cloro que é 73,9% de mercúrio e 26,1% de cloro em massa. Qual é a fórmula empírica?
Digamos que temos uma amostra de 100 gramas deste composto. Então, a amostra contém 73,9 gramas de mercúrio e 26,1 gramas de cloro. Quantos moles de cada átomo representam as massas individuais?
Para o Mercúrio:(73,9 g) x (1 mol/200,59 g) = 0,368 mol
Para o Cloro:(26,1 g) x (1 mol/35,45 g) = 0,736 mol
Qual é a relação molar entre os dois elementos?
(0,736 mol Cl/0,368 mol Hg) = 2,0
Assim, nós temos duas vezes mais moles (isto é, átomos) de Cl que de Hg. A fórmula empírica seria assim (lembre-se de colocar o cátion primeiro e o ânion por último): HgCl2 .
3. Massa molecular de uma substância – É a massa da molécula dessa substância expressa em u. Indica quantas vezes a massa da molécula dessa substância é maior que a massa de 1/12 do átomo de 12C.
A massa molecular de uma substância é numericamente igual à soma das massas atômicas de todos os átomos da molécula dessa substância.
Exemplo: para a molécula C12H22O11 (açúcar), a massa molecular será:
12 átomos de carbono = 12 x 12,0111 u = 144,133 u
22 átomos de hidrogênio = 22 x 1,0079 u = 22,174 u
11 átomos de oxigênio = 11 x 15,9994 = 175,993 u e a soma 342,3 u.
Mol
Um mol é definido como a quantia que contém tantos objetos quanto o número de átomos em exatamente 12 gramas de 12C.
Várias experiências determinaram que este número é 6,0221367 x 1023, ou simplesmente 6,022 x 1023, e é conhecido como o número de Avogadro. Um mol de átomos, carros, pessoas, etc... – contém 6,022 x 1023 destes objetos. Mas quão grande é este número? Um mol de gesso cobrindo a Terra resultaria em uma capa com 5 quilômetros de espessura.
Massa molar
Um único átomo 12C tem uma massa de 12u. Um único átomo de 24Mg (magnésio - 24) tem uma massa de 24u, ou duas vezes a massa de um átomo 12C. Assim, um mol de átomos 24Mg deveria ter a massa de duas vezes um mol de átomos 12C. Se um mol de átomos 12C tem massa 12 gramas (por definição), um mol de átomos 24Mg tem massa de 24 gramas.
Note que a massa de um átomo em unidades de massa atômica (u) é numericamente igual à massa de um mol dos mesmos átomos em gramas (g). A massa em gramas de 1 mol de uma substância é chamada massa molar. A massa molar (em gramas) de qualquer substância sempre é numericamente igual à sua massa de fórmula (em u).
Exs.: a) Uma molécula de H2O tem massa de 18,0 u; 1 mol de H2O pesa 18,0 gramas
b) Um íon NaCl tem massa de 58,5 u; 1 mol de NaCl tem massa de 58,5 gramas
c) Suponha uma amostra de 1,5 mol de cloreto de cálcio (a fórmula química do cloreto de cálcio é CaCl2). A massa atômica do Ca = 40,078u. A massa atômica do Cl = 35,453u. Então, a massa de fórmula do CaCl2 = (40,078) + 2 x (35,453) = 110,984u, (este composto é iônico, assim não há nenhuma “massa/peso molecular”). Então, um mol de CaCl2 tem uma massa de 110,984 gramas. Assim, 1,5 mol de CaCl2 vale:
(1,5 mol)x(110,984 gramas/mol) = 166,476 gramas
d) Em uma amostra de 2,8 gramas de ouro, quantos átomos existem ?
A fórmula molecular do ouro é: Au.
O Peso/Massa molecular do Au = 196,9665u.
Então, 1 mol de ouro tem massa de 196,9665 gramas. Assim, em 2,8 gramas de ouro temos:
196,9665g –––––––––– 1 mol
2,8g –––––––––––––––– X
X=0,0142mol
Cálculo estequiométrico:
O cálculo estequiométrico, apesar de temido por muitos vestibulandos, deixa de ser um problema se os seguintes passos forem seguidos:
1.° passo – Montar e balancear a equação química.
2.° passo – Escrever a proporção em mols (coeficientes da equação balanceada).
3.° passo – Adaptar a proporção em mols às unidades usadas no enunciado do exercício (massa, volume nas CNTP, n.° de moléculas etc).
4.° passo – Efetuar a regra de três com os dados do exercício.
Equações químicas
As reações que os elementos têm entre si para formar um composto são representadas por equações químicas. Exemplo da reação do hidrogênio com o oxigênio para formar água:
As substâncias no lado esquerdo são chamadas reagentes e, no lado direito, produtos. Os números antes dos símbolos (omitido se for 1) indicam a quantidade de moléculas. Os símbolos entre parênteses indicam o estado físico: (s) sólido, (l) líquido, (g) gasoso e (aq) solução aquosa (muitas substâncias só reagem em solução aquosa). Lembrar que a equação química indica a possibilidade de uma reação. Isto significa que a reação nem sempre ocorrerá com o simples contato físico das substâncias. Algumas precisam de aquecimento, outras,de meio aquoso, outras,de ignição (é o caso do exemplo),etc.
Uma equação química deve ser balanceada, isto é, cada elemento deve ter o mesmo número de átomos em ambos os lados da equação. No exemplo dado, esta condição está satisfeita. O balanceamento significa a necessária igualdade de massas entre os dois lados da equação uma vez que não pode haver perda ou ganho de massa.
Massa atômica, massa molecular
Em química, no lugar das unidades convencionais, a massa de um átomo é expressa em unidades de massa atômica (u) que equivale exatamente a 1/12 da massa do isótopo 12C (carbono 12). Na unidade comum, corresponde a 1,6605402 x 10-27 kg . Pelo fato de o carbono 12 possuir 6 prótons e 6 nêutrons, concluímos que a unidade de massa atômica é, aproximadamente, a massa de um próton ou de um nêutron(1 próton=1,0081u; 1 nêutron=1,0090u). O átomo de 12C foi escolhido como átomo padrão na construção das escalas de massas atômicas. Sua massa atômica foi fixada em 12u.
Unidade de massa atômica (u) é a massa de 1/12 do átomo de 12C.
Massa atômica de um átomo – É a massa desse átomo expressa em u. Indica quantas vezes a massa do átomo é maior que 1/12 da massa de 12C.
Massa atômica de um elemento – A massa atômica de um elemento é a massa média dos átomos desse elemento expressa em u. É igual à média ponderada das massas atômicas dos isótopos constituintes do elemento.
2. Tipos de cálculo estequiométrico
Através da quantidade de matéria em mols, massa em gramas, volume e número de moléculas, podemos expressar os problemas.
Isso são tipos de cálculos estequiométricos, onde podemos tirar por base os coeficientes da equação que apresentam a proporção em mols de todos os componentes da reação.
3. Relação massa-massa
Se tratando de massa teremos: dados do problema e quantidades incógnitas pedidas.
Por exemplo:
Na reação: 1N2(g) + 3H2(g) → 2NH3(g)
Se a NH3 reagisse por completo 3g de H2, qual seria sua massa?
Observe a resolução:

4. Cálculos estequiométricos em reações consecutivas
Para que possamos criar uma relação entre as quantidades de matéria de substâncias existentes nas reações consecutivas, é preciso que as equações químicas tenham uma substância em comum entre elas, apresentando assim coeficientes iguais nas equações.
Vejamos um por exemplo:
O ácido nítrico surge a partir e algumas reações observem a equação dessas reações.
1) 4NH3 + 5O2 → 4NO + 6H2O
2) 2NO + O2 → 2NO2
3) 3NO2 + H2O → 2HNO3 + NO
Agora, para calcular a massa da amônia é preciso para que ocorra a preparação de 6,3 gramas de ácido nítrico.
Dado:
Massas molares em g/mol:
NH3: 17
HNO3: 63
NO2: 46
NO: 30
Vejamos a resolução:
NH3, está presente na reação 1).
HNO3, está presente na reação 3).
NO, participa das reações 1) e 2).
NO2, está presente nas reações 2) e 3).
Efetuando a multiplicação da equação 2) por 2, e a equação 3) por 4/3, obteremos:
1) 4NH3 + 5O2 → 4NO + 6H2O
2) 4NO + 2O2 → 4NO2
3) 4NO2 + 4/3H2O → 8/3HNO3 + 4/3NO
É possível conseguir 8/3 mols de HNO3, a partir de 4 mols NH3.
Vejamos:
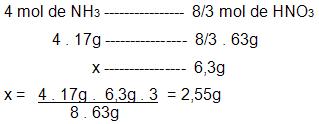
Resolução do problema sem executar o balanceamento da equação
- calculo da quantidade de NO2 que será preciso para adquirir 6,3g de HNO3.
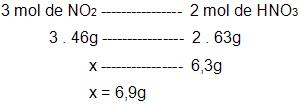
- cálculo da quantidade de NO que será preciso para adquirir 6,9g de NO2.
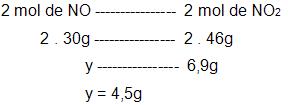
- cálculo da quantidade de NH3 que será preciso para adquirir 4,5g de NO.
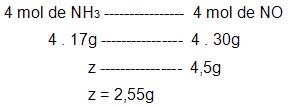
5. Relação massa-volumeNo problema a quantidade incógnita e a massa são expressas em volume. Para isso temos que lembrar que em 1 mol de qualquer um dos gases, a 1 atm e 0°C, irá ocupar um volume de aproximadamente 22,4 litros.
Vejamos um exemplo:
Na reação:
1N2(g) + 3H2(g) → 2NH3(g), qual seria o volume de N2 a 0°C e 1 atm, que iria reagir diretamente com 3g de H2?
Vejamos a resolução:

6. Reagentes em excesso Um reagente em excesso, expressa a sua quantidade no problema em questão, pois quando um reagente não está em excesso, aparece apenas a quantidade de um e também a quantidade de do outro a ser calculado. Caso o reagente limitante seja a base do cálculo estequiométrico, para podermos efetuá-lo, devemos determinar primeiramente o reagente que está em excesso.
Por exemplo:
Na reação:
2H2 + O2 → 2H2O
Se adicionarmos 3g de hidrogênio e 30g de oxigênio obteremos a seguinte massa:
Vejamos a resolução:

Essa reação resulta na sobra de 30g – 24g = 6g de O2 em excesso sem reagir, isso ocorre, pois, há no recipiente 30g de O2.

Ocorre uma que o reagente limita a quantidade formada de produto, esse limite é promovido pelo reagente que possui menor quantidade.
7. PurezaO conceito de pureza diz respeito ao fato de que algumas vezes as substâncias reagentes estão acompanhadas de impurezas.
Por exemplo:
CaCO3 de 80% de pureza;
Quer dizer que em 100g de CaCO3 impuro é a composição + areia + carvão, entre outras impurezas, tem-se 80g de CaCO3 puro, portanto de impurezas tem-se apenas 20g.
Desta forma se usarmos 150g de CaCO3 em uma reação, com 80% de pureza, iremos obter 120g, pois
8. Rendimento
O rendimento diz respeito à quantidade de produto formado, e que foi calculada de acordo com coeficientes.
Porém, o resultado obtido da quantidade de produto através da reação, não é o mesmo que se pretendia ao fazer o cálculo, pois o resultado é menor. Desta forma 90% é o rendimento adquirido.
Reação de 0º e 1 atm, 11, 2 litros de CO2 com hidroácido de sódio;
Sabendo que o rendimento da reação foi de 90%, qual a massa do carbono de sódio obtido?
CO2 + 2NaOH → Na2CO3 + H2O
- proporção de quantidade de matéria, coeficientes.
1mol de CO2 → 1mol de Na2CO2
- regra de três.
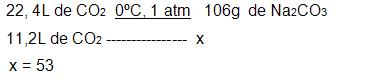
- massa de Na2CO3 com um rendimento de 100%
53g
- massa de Na2CO3 com um rendimento de 90%

Tomando como foco de calculo os coeficientes, o rendimento(R) é expresso da seguinte forma:
9. Utilização do conceito de equivalente nos cálculos estequiométricos
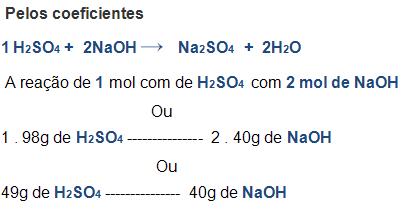
Para sabermos a resolução de alguns problemas envolvendo cálculos estequiométricos, usamos um conceito de equivalente e muito útil. Se tratando de equivalente, podemos criar uma regra de três, tirando todos os coeficientes da equação. Para que isso ocorra temos que saber que em toda reação, 1 equivalente irá reagir sempre com 1 equivalente.
Vejamos um exemplo:
Observe agora a neutralização do NaOH pelo H2SO4 das duas formas; conceito de equivalente e coeficientes, mas antes é importante saber que:

Vejamos agora das duas maneiras:

GASES PERFEITOS:
1. Introdução Como já sabemos a matéria pode apresentar três estados; sólido, líquido e gasoso.
As partículas no estado sólido estão distribuídas de forma regular e fixas, pelo fato de que estão fortemente ligadas.
As moléculas no estado líquido estão muito próximas, devido a uma força de atração evitando que as moléculas se separem. É importante sabermos que no estado líquido, os líquidos possuem forma de acordo com o recipiente em que eles estão, porém possuem volume definido.
As moléculas no estado gasoso estão ligadas por uma força de coesão muito fraca, por este fato elas estão se movimentando de maneira desordenada, e com velocidades variadas, os gases não possuem volume, eles ocupam todo o recipiente que estão, e não possuem forma e nem volume próprio.
Os gases exercem pressão, pois esse espaço que existe entre as moléculas e a forma com que elas se movimentam, resulta na alta compressibilidade do gás, e as moléculas dele, quando estão em recipiente bombardeiam as paredes dele.
2. Gases ideais ou perfeitos
Os gases são classificados em dois grupos devido à diferença de diversos aspectos, como por exemplo, a pressão, o volume etc. Vejamos:
1 – gases ideais ou perfeitos;
2 – gases reais.
O gás perfeito é regido sobre as leis de Boyle e Charles, que foram obtidas através de experiências de ambos, também é possível deduzi-las pela teoria cinética dos gases:
- em relação ao volume ocupado pelo gás perfeito, podemos dizer que esse volume é desprezível em relação ao volume ocupado por ele mesmo.
- independente da pressão e temperatura, não ocorre atração mutua entre moléculas.
3. Mudanças de estado: leis que as regem
A pressão, o volume e a temperatura são o que definem uma massa gasosa.
Essas variáveis de estado sofrem alterações, que resultam em uma transformação ou mudança de estado do gás.
Se classificarmos as transformações que ocorrem mais freqüentes no gás teremos:
Isotérmicas;
Isobárica:
Isométrica ou isocórica, dependendo se a temperatura será constante.
Para sabermos a resolução de alguns problemas envolvendo cálculos estequiométricos, usamos um conceito de equivalente e muito útil. Se tratando de equivalente, podemos criar uma regra de três, tirando todos os coeficientes da equação. Para que isso ocorra temos que saber que em toda reação, 1 equivalente irá reagir sempre com 1 equivalente.
Vejamos um exemplo:
Observe agora a neutralização do NaOH pelo H2SO4 das duas formas; conceito de equivalente e coeficientes, mas antes é importante saber que:

Vejamos agora das duas maneiras:


GASES PERFEITOS:
1. Introdução Como já sabemos a matéria pode apresentar três estados; sólido, líquido e gasoso.
As partículas no estado sólido estão distribuídas de forma regular e fixas, pelo fato de que estão fortemente ligadas.
As moléculas no estado líquido estão muito próximas, devido a uma força de atração evitando que as moléculas se separem. É importante sabermos que no estado líquido, os líquidos possuem forma de acordo com o recipiente em que eles estão, porém possuem volume definido.
As moléculas no estado gasoso estão ligadas por uma força de coesão muito fraca, por este fato elas estão se movimentando de maneira desordenada, e com velocidades variadas, os gases não possuem volume, eles ocupam todo o recipiente que estão, e não possuem forma e nem volume próprio.
Os gases exercem pressão, pois esse espaço que existe entre as moléculas e a forma com que elas se movimentam, resulta na alta compressibilidade do gás, e as moléculas dele, quando estão em recipiente bombardeiam as paredes dele.
2. Gases ideais ou perfeitos
Os gases são classificados em dois grupos devido à diferença de diversos aspectos, como por exemplo, a pressão, o volume etc. Vejamos:
1 – gases ideais ou perfeitos;
2 – gases reais.
O gás perfeito é regido sobre as leis de Boyle e Charles, que foram obtidas através de experiências de ambos, também é possível deduzi-las pela teoria cinética dos gases:
- em relação ao volume ocupado pelo gás perfeito, podemos dizer que esse volume é desprezível em relação ao volume ocupado por ele mesmo.
- independente da pressão e temperatura, não ocorre atração mutua entre moléculas.
3. Mudanças de estado: leis que as regem
A pressão, o volume e a temperatura são o que definem uma massa gasosa.
Essas variáveis de estado sofrem alterações, que resultam em uma transformação ou mudança de estado do gás.
Se classificarmos as transformações que ocorrem mais freqüentes no gás teremos:
Isotérmicas;
Isobárica:
Isométrica ou isocórica, dependendo se a temperatura será constante.
4. Transformação isotérmica
Ocorre quando a temperatura fica constante durante a transformação.
A lei de Boyle – Mariotte, quantitativamente explica a compressibilidade do gás.
Certa massa de gás ocupa certo volume, contrariamente proporcional à sua pressão. Isso ocorre à temperatura constante.
Estado 1
Massa: m
Pressão: P1
Volume: V1
Temperatura: T1
Estado 2
Massa: m
Pressão: P2 = 2P1
Volume: V2 = 1/2V1
Temperatura: T2 = T1
Expressão algébrica da lei:
PV = constante
P1 V1 = P2 V2 = P3 V3...
6. Transformação isocórica (ou isométrica)
Lei de Gay-Lussac: o volume permanece constante.
A pressão de certa massa de gás será totalmente proporcional à temperatura exata, a volume constante.
Estado 1
Massa: m
Volume: V1
Pressão: P1
Temperatura: T1
Estado 2
Massa: m
Volume: V2 = V1
Pressão: P2 = 2P1
Temperatura: T2 = 2T1
Expressão algébrica da lei:
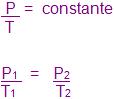
Expressão algébrica da lei:
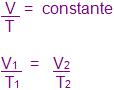
8. Equação de ClapeyronOcorre quando a temperatura fica constante durante a transformação.
A lei de Boyle – Mariotte, quantitativamente explica a compressibilidade do gás.
Certa massa de gás ocupa certo volume, contrariamente proporcional à sua pressão. Isso ocorre à temperatura constante.
Estado 1
Massa: m
Pressão: P1
Volume: V1
Temperatura: T1
Estado 2
Massa: m
Pressão: P2 = 2P1
Volume: V2 = 1/2V1
Temperatura: T2 = T1
Expressão algébrica da lei:
PV = constante
P1 V1 = P2 V2 = P3 V3...
5. Transformação isobárica
Relativa à Lei de Charles, a pressão fica constante durante a transformação.
Todo o volume que ocupar certa massa de um gás será diretamente proporcional à sua temperatura exata. Isso ocorre à pressão constante.
Estado 1
Massa: m
Pressão: P1
Volume: V1
Temperatura: T1
Estado 2 Massa: m
Pressão: P2 = P1
Volume: V2 = 2V1
Temperatura: T2 = 2T1
Relativa à Lei de Charles, a pressão fica constante durante a transformação.
Todo o volume que ocupar certa massa de um gás será diretamente proporcional à sua temperatura exata. Isso ocorre à pressão constante.
Estado 1
Massa: m
Pressão: P1
Volume: V1
Temperatura: T1
Estado 2 Massa: m
Pressão: P2 = P1
Volume: V2 = 2V1
Temperatura: T2 = 2T1
Expressão algébrica da lei:
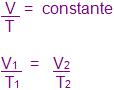
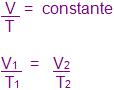
Lei de Gay-Lussac: o volume permanece constante.
A pressão de certa massa de gás será totalmente proporcional à temperatura exata, a volume constante.
Estado 1
Massa: m
Volume: V1
Pressão: P1
Temperatura: T1
Estado 2
Massa: m
Volume: V2 = V1
Pressão: P2 = 2P1
Temperatura: T2 = 2T1
Expressão algébrica da lei:
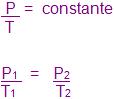
5. Transformação isobárica
Relativa à Lei de Charles, a pressão fica constante durante a transformação.
Todo o volume que ocupar certa massa de um gás será diretamente proporcional à sua temperatura exata. Isso ocorre à pressão constante.
Estado 1
Massa: m
Pressão: P1
Volume: V1
Temperatura: T1
Estado 2 Massa: m
Pressão: P2 = P1
Volume: V2 = 2V1
Temperatura: T2 = 2T1
7. Equação geral dos gases perfeitos Considerando um gás representado por G, que vai do estado 1 para o estado 2, teremos:
Estado 1
Massa: m
Volume: V1
Pressão: P1
Temperatura: T1
Estado 2
Massa: m
Volume: V2
Pressão: P2
Temperatura: T2
Relativa à Lei de Charles, a pressão fica constante durante a transformação.
Todo o volume que ocupar certa massa de um gás será diretamente proporcional à sua temperatura exata. Isso ocorre à pressão constante.
Estado 1
Massa: m
Pressão: P1
Volume: V1
Temperatura: T1
Estado 2 Massa: m
Pressão: P2 = P1
Volume: V2 = 2V1
Temperatura: T2 = 2T1
7. Equação geral dos gases perfeitos Considerando um gás representado por G, que vai do estado 1 para o estado 2, teremos:
Estado 1
Massa: m
Volume: V1
Pressão: P1
Temperatura: T1
Estado 2
Massa: m
Volume: V2
Pressão: P2
Temperatura: T2
Expressão algébrica da lei:
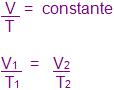
É possível o gás passar por um estado intermediário (3), observe o diagrama:
(1) → (2) → (3)
Desta forma teremos:

A Lei de Boyle e Charles aplica:
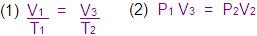
Se multiplicar parte por parte
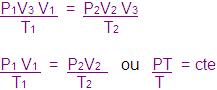
(1) → (2) → (3)
Desta forma teremos:

A Lei de Boyle e Charles aplica:
Se multiplicar parte por parte
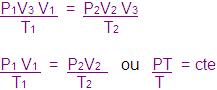
Constante universal dos gases perfeitos é o valor de um mol de gás na constante de PV/T igual para qualquer gás.
Para um mol de qualquer gás
Para n mols.
Valores numéricos de R

GASES PERFEITOS-2:
1. Misturas de gases perfeitos O fato de que os gases são miscíveis, independente da proporção resulta em misturas gasosas homogêneas.
2. Pressão parcial A pressão parcial de um gás ocorre quando ele exerce em uma mistura gasosa, uma pressão que normalmente seria exercida, caso a temperatura da mistura fosse à mesma, e ocupasse todo o seu volume.
Considere essa mistura:
gases Z;
Recipiente de volume V;
Pressão P;
Temperatura T.
Onde o gás i irá ocupar sozinho o volume V, a temperatura T, a sua própria pressão que podemos chamar de pi, logo que por definição é a pressão parcial do gás i.
Observe:
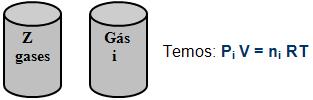
V, T, P V, T, Pi
Ni = quantidade em mols do gás i.
3. Volume parcial
O volume parcial de um gás ocorre quando sobre uma pressão igual à pressão total da mistura, e sobre uma temperatura igual à mistura, onde o gás ocuparia esse volume.
A partir da mistura de Z gases anteriores, onde o volume que o gás i ocupa na pressão P e temperatura T, onde o volume vi é o volume parcial do gás i.
Teremos:
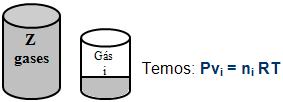
P, V, T P, Vi, T
4. Fração em mol
Abaixo a fração do mol expressa na relação:
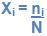
Onde:
ni – quantidade em mols de gás i.
n – quantidade em mols da mistura.
Obtemos:
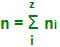
Por exemplo:
Observe a mistura:
1 mol de H2
1,5 mol de N2
2,5 mol de CO2
Teremos:
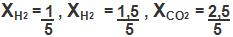
Abaixo a fração do mol expressa na relação:
Onde:
ni – quantidade em mols de gás i.
n – quantidade em mols da mistura.
Obtemos:
Por exemplo:
Observe a mistura:
1 mol de H2
1,5 mol de N2
2,5 mol de CO2
Teremos:
6. Lei de Amagat
Segundo essa lei, a soma dos volumes parciais de seus componentes, é ocupada por uma mistura gasosa.
V = v1 + v2 + v3 + ... vz
Segundo essa lei, a soma dos volumes parciais de seus componentes, é ocupada por uma mistura gasosa.
V = v1 + v2 + v3 + ... vz
7. Relação entre pressão total, pressão parcial e fração em mol (Xi)
Temos: PV = nRT e piV = ni RT
Divisão parte a parte:
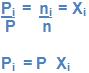
Em uma mistura gasosa a pressão parcial de um gás é igual ao resultado de sua fração em mol na mistura, pela própria pressão.
Observe a semelhança:
vi = V . Xi
Temos: PV = nRT e piV = ni RT
Divisão parte a parte:
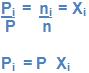
Em uma mistura gasosa a pressão parcial de um gás é igual ao resultado de sua fração em mol na mistura, pela própria pressão.
Observe a semelhança:
vi = V . Xi
8. Pressão da mistura e pressão dos gases componentes antes de misturar
Os gases antes da mistura
Observe os gases G1 e G2, nos seguintes estados:
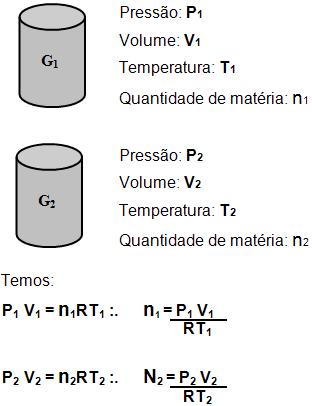
Os gases depois da mistura
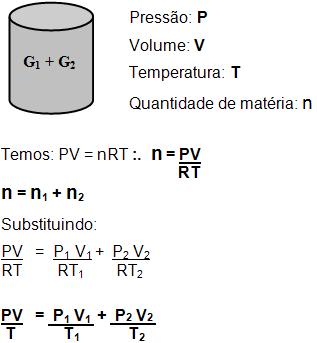
9. Densidade dos gases A relação entre a massa e o volume é que determina a densidade de uma substância (d ou u).
Normalmente a densidade dos sólidos e líquidos são expressas em g/L, por exemplo, o gás cloro possui densidade de 25ºC e atm, isto é 2,92g/L.
10. Densidade absoluta ou massa específica de um gás
A densidade absoluta ou massa específica de um gás é determinada pela pressão e temperatura de um quociente existente entre a massa do gás e um volume de dele.
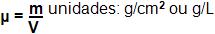
Veja agora em condições normais:

Em determinada temperatura:

A densidade é proporcional a sua própria pressão, já à sua temperatura absoluta é contrariamente proporcional.
A densidade absoluta ou massa específica de um gás é determinada pela pressão e temperatura de um quociente existente entre a massa do gás e um volume de dele.
Veja agora em condições normais:

Em determinada temperatura:

A densidade é proporcional a sua própria pressão, já à sua temperatura absoluta é contrariamente proporcional.
11. Densidade relativa do gás G1 em relação ao gás G2
A densidade relativa entre esses gases (G1 G2) é o quociente existente entre a densidade exata de G1 e a densidade exata de G2, que foram medidas com a mesma pressão e temperatura.
Observe:
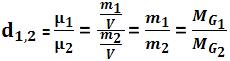
Contudo a densidade relativa não depende a pressão e da temperatura.
Em relação ao ar
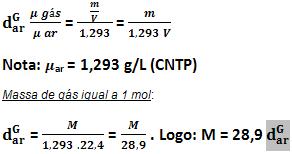
Densidade do gás em relação ao hidrogênio
Independente da pressão e da temperatura teremos:
Observe:
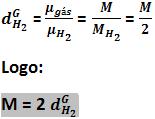
12. Difusão e efusão gasosa
Considerando que um recipiente contenha gás, se seu cheiro se espalhar todos que estarão ao redor, iram sentir o cheiro forte do gás (fato muito conhecido). Esse fato ocorre, pois as moléculas de um gás se movimentam com facilidade através dos espaços vazios entre as moléculas, fazendo com que elas se misturem uniformemente com eles.
Podemos pensar também que essas moléculas podem atravessar as paredes porosas, porém nem todas na mesma velocidade, independente se os gases estão ou não nas mesmas condições de temperatura e pressão.
Difusão gasosa – é a forma na qual, os gases atravessam uma parede porosa, e nesse mesmo processo se misturam de maneira uniforme com outros gases.
Porém, a efusão gasosa é conceituada como uma forma em que um gás escapa de um recipiente, por meio de um pequeno furo, para o vácuo.
Thomas Graham foi um químico britânico, que estudou a efusão gasosa, ele criou a lei que o explica.
“As velocidades de efusão dos gases são inversamente proporcionais às raízes quadradas de suas massas específicas, quando submetidos à mesma pressão e temperatura.”
13. Condições normais de temperatura e pressão (CNTP)
A temperatura normal à alguns anos atrás era 0°C, já a pressão normal era de 1 atm. Considerando esses valores, temos que o volume molar dos gases é 22,4 L.
Onde:
T = 0ºC = 273K
P = 1 atm = 760mmHg = 101325Pa
Volume dos gases = 22,4L/mol
Atualmente a IUPAC modificou o valor pressão normal para 100000Pa. A 0ºC e 100000Pa o volume de 1 mol de gás é 22,7L.
Observe:
CNTP
P = 100000Pa → volume molar dos gases = 22,7/molar.
LEIS DAS COMBINAÇÕES:
1. Introdução
São resultados de experiências e comprovações efetuadas em laboratório as leis das reações químicas, ou seja, são leis empíricas ou experimentais, que surgiram no final do século XVIII, e início do século XIX.
Essas leis explicam o surgimento das idéias de átomos, moléculas, fórmula e equações químicas, por este fato as leis vão ser apresentadas de forma em que não seja preciso a utilização de fórmulas.
As leis que relacionadas à massa, leis ponderais:
1- Lei da conservação da massa ( ou de Lavoisier)
2- Lei das proporções constantes (ou de Proust)
3- Lei das proporções múltiplas (ou de Dalton)
4- Lei das proporções recíprocas (ou de Richter Wenzel)
As leis que estão relacionadas aos volumes gasosos são as leis volumétricas de Gay-Lussac. As leis ponderais trabalham com massas.
2. Lei da conservação da massa ou lei de Lavoisier
“Numa reação química a massa dos reagentes é igual à massa total dos produtos dessa reação.”
Para que possa comprovar experimentalmente a lei de Lavoisier é preciso que:
- Ligam-se duas ampolas de vidro por tubo de vidro, (observe a figura a seguir);
- Adiciona-se em uma das ampolas solução de um reagente (A), e na outra solução de um reagente (B);
- Fecham-se as ampolas hermeticamente, “a fogo”, e depois eles são pesados.
- para que as soluções se misturem o conjunto deve ser virado “de cabeça para baixo”
A + B → C + D
Por exemplo:
NaCl + AgNO3 → AgCl + NaNO3
- Após misturar, pesa-se outra vez.
A pesar da reação química, a massa final é igual à massa inicial.
3. Lavoisier – o fundador da Química Moderna
A lei da conservação da massa (na natureza nada se cria, nada se perde, tudo se transforma) está relacionada ao nome de um químico muito famoso, Antoine Laurent Lavoisier, que é considerado o criador da Química Moderna, graças ao seu equipamento e materiais de ótima qualidade que evitavam erros nos estudos e resultava um trabalho com mais precisão.
O ano de 1789 ficou marcado com a publicação do livro Traité Elémentaire de Chimie, de Lavoisier, que fortaleceu o processo de revolução química.
Foi através de experiência em sistemas fechados, onde os gases eram impedidos de tornarem-se livres, que Lavoisier pode comprovar sua tese da conservação da massa.
Lavoisier permitiu que a matéria fosse constituída por princípios ou elementos, onde havia um elemento imponderável denominado calórico. Sendo assim, dois elementos seriam constituintes do gás oxigênio: o oxigênio e o calórico.

A lei da conservação da massa (na natureza nada se cria, nada se perde, tudo se transforma) está relacionada ao nome de um químico muito famoso, Antoine Laurent Lavoisier, que é considerado o criador da Química Moderna, graças ao seu equipamento e materiais de ótima qualidade que evitavam erros nos estudos e resultava um trabalho com mais precisão.
O ano de 1789 ficou marcado com a publicação do livro Traité Elémentaire de Chimie, de Lavoisier, que fortaleceu o processo de revolução química.
Foi através de experiência em sistemas fechados, onde os gases eram impedidos de tornarem-se livres, que Lavoisier pode comprovar sua tese da conservação da massa.
Lavoisier permitiu que a matéria fosse constituída por princípios ou elementos, onde havia um elemento imponderável denominado calórico. Sendo assim, dois elementos seriam constituintes do gás oxigênio: o oxigênio e o calórico.

4. Lei das produções constantes (ou proporções fixas, definidas) ou lei de Proust.
Considerando que uma reação química foi realizada em várias experiências, podemos dizer que a proporção existente entre as massas dos reagentes ou entre as massas dos produtos são constantes.
Por exemplo:
A água independente de sua procedência será sempre formada por hidrogênio e oxigênio (na proporção de 1g de hidrogênio para 8g de oxigênio).
A lei de Proust pode ser comprovada, por exemplo, se usarmos a água, para isso será necessário que: - recolher amostras de água de várias procedências, por exemplo, da chuva, de rios etc.
- purificar as amostras que foram recolhidas o máximo que for possível.
- decompõe cada amostra da água e pesa-se o hidrogênio e do oxigênio.
A partir daí vamos obter diversos valores, como por exemplo:

É constante a proporção da entre as massas de hidrogênio e oxigênio.
Proporção 1 : 8 As massas são distintas, porém, a proporção entre as massas de hidrogênio e de oxigênio é sempre constante, fixa e definida ou invariável, ou seja, na água a massa do oxigênio e sempre oito vezes mais (1 :8) que a do hidrogênio.
De maneira geral, a proporção pode ser pensada como:

5. Conseqüências da lei de Proust
- composição centesimal ou fórmula porcentual. São as porcentagens em massa que se referem aos elementos formadores dos compostos, ou seja, pode ser as massas dos elementos que resultam na formação de 100g do composto considerado, isso se refere a fórmula porcentual.
A regra de três será o cálculo da composição centesimal. 1g de hidrogênio é encerrado por 9g de água, logo, 100g de água é encerrarão “x” g de hidrogênio.
Ocorre mudança apenas dos números, porém mantendo a proporção.
x = 11,11% de hidrogênio 8g de hidrogênio é encerrado por 9g de água, e 100g de água encerrarão “y” g de oxigênio, logo teremos:
y = 88,98% de oxigênio
Desta forma a composição centesimal da água é:
11,11% de hidrogênio
88,89% de oxigênio
- composição centesimal ou fórmula porcentual. São as porcentagens em massa que se referem aos elementos formadores dos compostos, ou seja, pode ser as massas dos elementos que resultam na formação de 100g do composto considerado, isso se refere a fórmula porcentual.
A regra de três será o cálculo da composição centesimal. 1g de hidrogênio é encerrado por 9g de água, logo, 100g de água é encerrarão “x” g de hidrogênio.
Ocorre mudança apenas dos números, porém mantendo a proporção.
x = 11,11% de hidrogênio 8g de hidrogênio é encerrado por 9g de água, e 100g de água encerrarão “y” g de oxigênio, logo teremos:
y = 88,98% de oxigênio
Desta forma a composição centesimal da água é:
11,11% de hidrogênio
88,89% de oxigênio
6. Lei de Dalton
"Em uma mistura gasosa, a pressão de cada componente é independente da pressão dos demais, a pressão total (P) é igual à soma das pressões parciais dos componentes."
Pt = P1 + P2 + ... + Pn
Exemplo: Sabemos que o ar atmosférico é composto essencialmente, na prática, de 78,8% de Nitrogênio e de 20,95% de oxigênio. Assim sendo, e aplicando-se a Lei de Dalton, podemos dizer que a expressão total do ar atmosférico, 760 mmHg ao nível do mar, é representada em seu 1/5 pela pressão parcial de oxigênio. Então podemos dizer que.
Pt (760 mmHg) = Tp O2 150) + Tp N≈(1/5 de 760 2 (4/5 de 760 ≈593)
Resumindo: A tensão parcial de O2 ao nível do mar é 152 mmHg e a tensão parcial do N2 ao mesmo nível é de 608 mmHg.
"Em uma mistura gasosa, a pressão de cada componente é independente da pressão dos demais, a pressão total (P) é igual à soma das pressões parciais dos componentes."
Pt = P1 + P2 + ... + Pn
Exemplo: Sabemos que o ar atmosférico é composto essencialmente, na prática, de 78,8% de Nitrogênio e de 20,95% de oxigênio. Assim sendo, e aplicando-se a Lei de Dalton, podemos dizer que a expressão total do ar atmosférico, 760 mmHg ao nível do mar, é representada em seu 1/5 pela pressão parcial de oxigênio. Então podemos dizer que.
Pt (760 mmHg) = Tp O2 150) + Tp N≈(1/5 de 760 2 (4/5 de 760 ≈593)
Resumindo: A tensão parcial de O2 ao nível do mar é 152 mmHg e a tensão parcial do N2 ao mesmo nível é de 608 mmHg.
7. Lei das proporções recíprocas o lei de Richter – Welzel – berzelius.
Essa lei refere-se à massa fixa de ma de um elementos A que é combinado com as massas mb e mc dos elementos B e C, respectivamente, se acaso B e C combinarem entre si, usaram as massas m’b e m’c de maneira que:

É necessária extrema atenção, pois essa lei é bastante complexa, observe o seguinte esquema, que se trata de três elementos químicos A, B C.
Observe:
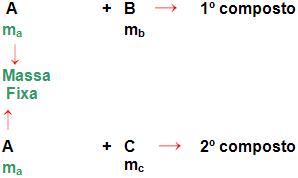
Caso B e C reagirem entre si, pode-se concluir que:

Onde teremos:
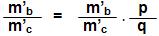
onde p e q serão números inteiros, em geral, pequenos.
Vejamos um exemplo:
Verificando por meio de experiências, que:
6g de carbono + 2g de hidrogênio → metano
6g de carbono + 71g de cloro → tetracloreto de carbono
Foi verificado também, que:
2g de hidrogênio + 71g de cloro → gás clorídrico
Neste composto estão combinados, hidrogênio e cloro na proporção (2 : 71), e se haviam combinado na massa fixa (6g) de carbono, desta forma o resultado correspondente é:
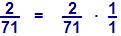
Essa lei refere-se à massa fixa de ma de um elementos A que é combinado com as massas mb e mc dos elementos B e C, respectivamente, se acaso B e C combinarem entre si, usaram as massas m’b e m’c de maneira que:

É necessária extrema atenção, pois essa lei é bastante complexa, observe o seguinte esquema, que se trata de três elementos químicos A, B C.
Observe:

Caso B e C reagirem entre si, pode-se concluir que:
Onde teremos:
onde p e q serão números inteiros, em geral, pequenos.
Vejamos um exemplo:
Verificando por meio de experiências, que:
6g de carbono + 2g de hidrogênio → metano
6g de carbono + 71g de cloro → tetracloreto de carbono
Foi verificado também, que:
2g de hidrogênio + 71g de cloro → gás clorídrico
Neste composto estão combinados, hidrogênio e cloro na proporção (2 : 71), e se haviam combinado na massa fixa (6g) de carbono, desta forma o resultado correspondente é:
8. Conseqüência da lei de Richter
Uma das conseqüências dessa lei, das proporções recíprocas, é em relação ao conceito de equivalente-grama de um elemento químico. É importante lembrarmos que esse conceito serve também para os compostos químicos.
Vejamos um exemplo:
Considere o primeiro exemplo dado: 2g de hidrogênio e 71g de cloro combinaram-se separadamente, com 6g de carbono, caso ocorra uma reação das duas massas entre si, pode-se dizer que: 2g de hidrogênio e 71g de cloro se equivalem do ponto de vista químico, mesmo sendo diferentes entre si e com um padrão de comparação de 6g de carbono.
8g de oxigênio é o padrão mais utilizado nos cálculos dos equivalentes-gramas em Química.
Por esse motivo é que podemos dizer que a massa de um elemento que se combina com 8g de oxigênio, é o equivalente-grama desse mesmo elemento químico.9. Lei de volumétrica de Gay – Lussac

A lei de Gay-Lussac diz respeito à reação dos gases entre si, e os volumes são medidos nas mesmas condições de pressão e temperatura, existe também, uma razão de números inteiros, geralmente pequenos, existentes entre os volumes dos gases reagentes e os produtos de reação.
Primeiro exemplo (todos os gases)
1 N2 + 3 H2 → 2 NH3
1VN2 : 3V H2 : 2VNH3
Segundo exemplo (todos os gases)
2C4H10 + 13O2 → 8CO2 + 10H2O
2VC4H10 : 13VCO2 : 8VCO2 : 10VH2O
Caso a água esteja no estado líquido, vale apenas:
2VC4H10 : 13VO2 : 8VCO2
Contração de volume (em reação entre gases)
A diferença entre a soma dos volumes dos gases reagentes e o volume do gás resultante, é a contração.
C = S – V
Onde:
S = soma dos volumes dos gases que se combinam.
V = volume do gás resultante.
A fração do volume inicial que diminui é a contração relativa.
Exemplo:

fonte: http://www.colegioweb.com.br/quimica





Nenhum comentário:
Postar um comentário